Springerproblem, Rösselsprung, Rösselsprungrätsel |
Ein Springerproblem (auch Rösselsprung genannt) ist ein Problem der Kombinatorik und nicht zu verwechseln mit dem Rösselsprungrätsel. Dabei muss für einen einzelnen Springer auf dem Schachbrett eine Route gefunden werden, auf der dieser jedes Schachfeld genau einmal besucht. Die Tour ist geschlossen, wenn das Endfeld des Springers einen Springerzug vom Startfeld entfernt ist. Anderenfalls heißt der Weg offen.
Die Anfänge des Rösselsprungs liegen in China ca. 2200 vor Christi Geburt.
840 entstanden die ersten rösselsprungartigen Aufzeichnungen auf 64 Feldern in den
Manuskripten der beiden arabischen Schachspieler Al-Adli (Al-Ádlí ar-Rúmí) und
Ali Ibn Mani.
900 wurde der früheste indische Rösselsprung von dem aus Kaschmir
stammenden Poeten Rudrata aufgezeichnet. Es
erschienen auf je einer Hälfte des Schachbrettes zwei gleiche Diagramme. Der
Titel seines Werkes lautet Kavyalankara.
946 erschienen die ersten symmetrischen Rösselsprünge in den Manuskripten des arabischen Schachgelehrten
as-Suli (Abu Bakr Muhammad bin Yahya as-Suli) analog zu den 64zeiligen Gedichten von
Ibn Duraid
(Abu Bakr Muhammad ibn al-Hasan ibn Duraid al-Azdi). Die ersten beiden Buchstaben einer jeden Gedichtzeile
geben die
Koordinaten auf dem Schachbrett an.
1150 entstand der sogenannte Fürstenspiegel (auch manasollasa = Freude des
Geistes) für den indischen König Somesvara III, verknüpft mit einem
Huldigungsgedicht an den König.
1275 Nachweis eines ersten Rösselsprungs in Europa in einem mittelalterlichen Manuskript in anglonormannischer Sprache.
1325 folgte ein Manuskript von Nicolas de Nicolai in lateinischer Sprache.
1352 entstand ein Manuskript von Schams ad-Din Muhammad al-Amuli für die
persische Enzyklopädie "Nafa’iz al-Funun" ("Wertvolle Seiten der Wissenschaften"
oder auch "Schatz der
Wissenschaften").
Nach 1500 fanden sich meist über das halbe Schachbrett angelegte Rösselsprünge
in den ersten europäischen Schachbüchern in Italien und gerieten dann für mehr
als zwei Jahrhunderte in Vergessenheit. Erst am Anfang des 18. Jahrhunderts
begann in Europa die wissenschaftliche und mathematische Analyse des
Rösselsprungs. Die Ergebnisse der Mathematiker Raimond de Montmort, Abraham de
Moivre and Jean-Jacques de Mairan wurden in vier Bänden von Claude Jombert 1725
in Paris herausgegeben.
1759 erforschte der Schweizer Mathematiker Leonhard Euler (1707 - 1783) das
Springerproblem mathematisch auf 5 x 5 Feldern.
1766 erschien das wunderschön gedruckte Buch "La Corso del Cavallo" von Lelio dalla Volpe in Bologna
1766.
1769 baute Kempelen seinen Schachautomaten, der unter anderem auch einen
Rösselsprung demonstrieren kann. Die Zuschauer konnten das Startfeld des
Springers frei wählen.
1771 präsentierte der französischer Musiker, Mathematiker und Chemiker Alexandre-Théophile Vandermonde (1735 - 1796) seine Arbeiten zum Springerproblem
an der Pariser Akademie der Wissenschaften.
1773 veröffentlichte Cosimo Alessandro Collini (1727 - 1806), der zu dieser Zeit
persönlicher Sekretär des Kurfürsten von der Pfalz war, sein Buch über den
Rösselsprung in Mannheim.
Hier eine kurze Auswahl:
1826 behandelte C. R. R. von Schinnern das Springerproblem in seinem Buch
"Ein Dutzend mathematischer
Betrachtungen", erschienen in Wien 1826.
1836 widmete sich Teodoro Ciccolini, Marchese di Guardiagrele, dem Thema
Rösselsprünge in seinem Buch "Del Cavallo degli Scacchi", erschienen in Paris
1836.
1839 wurde in Deutschland die Auflösung eines Rösselsprunges im Brockhaus Bilder-Conversations-Lexikon, Band 3. Leipzig 1839, S. 748-749 ausführlich
dargestellt.
1840 publizierte Peter Mark Roget im Philosophical Magazine in London seine Idee
von der Unterteilung der 64 Schachbrettfelder in vier separate Systeme, die
miteinander vernetzt sind.
1842 Das französische Schachmagazin "Le Palamède" enthält in der Ausgabe Nummer 13
vom 15. Dezember eine Abhandlung über Springerprobleme und zeigt unter anderem
die folgenden Abbildungen:
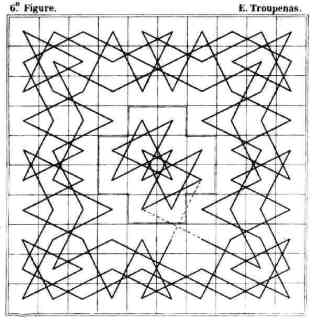
Eugène-Théodore Troupenas (1799-1850) war ein Mathematiker und Musikverleger in Paris.
1845 publizierte Charles Tomlinson Rösselsprünge in seinem Buch Amusements in
Chess.
1845 veröffentlichte die Leipziger Illustrirte Zeitung in der Ausgabe Nr. 111 vom
16. August 1845 oberhalb der Schachspalte unter der Überschrift
Wissenschaftliche Aufgaben die erste Rösselsprungaufgabe. Solche Aufgaben zähle
ich zu den Rösselsprungrätseln, die in der zweiten Hälfte des 19. Jahrhunderts
in illustrierten Ausgaben von Zeitungen, Zeitschriften und Familienmagazinen
ihre Blüte hatten.
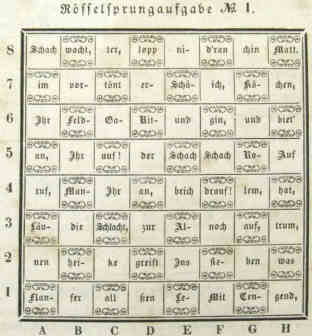
Die Lösung dieser Aufgabe finden Sie am Ende dieser Seite
1848 schrieb die Berliner Schachzeitung auf Seite 416 etwas zur Beziehung zwischen dem Mathematiker Leonhard Euler und dem Schachspieler Philidor. Ein Altonaer Freund teilte der Zeitung folgendes mit:
"Ich fand in der von dem Staatsrath Fuss*) herausgegebenen Correspondenz Eulers und anderer berühmten gleichzeitigen Mathematiker (Correspondance Mathématique et Physique de célèbres Géomètres du XVIIIème Siècle. St. Petersbourg 1843) im ersten Theile p. 545 eine Nachricht über Philidor, die Sie vielleicht interessiert, und die in einem mit tieferen mathematischen Untersuchungen angefüllten Buche Niemand so leicht suchen wird. Euler schreibt aus Berlin 1751 den 3. Juli an Goldbach*):
'Den großen Schachspieler Philidor habe ich nicht gesehen, weil er sich mehrenteils in Potsdam aufhielt. Er soll noch ein sehr junger Mensch sein, führte aber eine Maitresse mit sich, wegen welcher er mit einigen Offizieren in Potsdam Verdrießlichkeiten bekommen, welche ihn genötiget unvermutet wegzureisen; sonsten würde ich wohl Gelegenheit gefunden haben mit ihm zu spielen. Er hat aber ein Buch vom Schachspiel in England drucken lassen, welches ich habe und darin gewiss sehr schöne Arten zu spielen enthalten sind. Seine größte Stärke besteht in der Verteidigung und guter Führung seiner Bauern, um dieselben zu Königinnen zu machen, da er dann, wenn die Anstalten dazu gemacht, pièce für pièce wegnimmt, um seine Absicht zu erreichen und dadurch das Spiel zu gewinnen.'
"Euler muss, da er Philidor als großen Schachspieler kennt, und doch gerne mit ihm gespielt hätte, selbst eine bedeutende Stärke in unserem edelem Spiele gehabt haben."
*) Paul Heinrich Fuss (1798 - 1855 auch Fuss, Pavel Nikolaevich ) war ein
Urenkel Leonhard Eulers und Konferenzsekretär der Petersburger Akademie.
*) Christian Goldbach (1690 Königsberg - 1764 Moskau) war ein deutscher
Mathematiker. Die Goldbachsche Vermutung gehört zu den ältesten und
bedeutendsten ungelösten Problemen der Zahlentheorie.
1849 erschien in der Februar/März Ausgabe der Berliner Schachzeitung ein
Bericht von Otto von Oppen unter der Überschrift William Beverly's Rösselsprung
(Seiten 21 - 24 mit 5 Diagrammen) und auf den Seiten 41 - 97 folgen von Carl
Wenzelides die Bemerkungen über den Rösselsprung und Der Rösselsprung in
höchster Kunstvollendung (Seiten 41 - 97 mit 72 Diagrammen) und im Jahre 1850
folgte ab Seite 230 der zweite und letzte Teil der Bemerkungen mit weiteren 114
Diagrammen.
1855 schreibt Ernst Falkbeer in seiner Wiener Schachzeitung zum Thema
Rösselsprung Folgendes:
Wir möchten den Rösselsprung, dem ein Euler, ein Collini*), ein Warnsdorf*) ihre Aufmerksamkeit zugewendet haben, keineswegs für ein unfruchtbares, zeitraubendes und geisttötendes Spiel erklären, wie es so Manche tun, sondern ihn weit eher auf ein Niveau mit den edelsten Hervorbringungen des menschlichen Geistes stellen...
Der mathematische Scharfsinn wird hier auf die Probe gestellt, und die wichtige Gabe des Überschauens und des ruhigen anhaltenden Nachdenkens ist hier eben so am Platze, wie bei dem edlen Schachspiele selbst. Und endlich gewährt der Rösselsprung gleich jedem andern Spiele auch so manches Vergnügen. Denn trefflich zu gebrauchen sind seine verschiedenen Formen zur Aufgabe von scherzhaften Gedichten, Rätseln und der gleichen mehr. Und nimmt man hierzu die gefälligen und schönen Formen, die sich dem Auge darbieten, wenn das in Dunkel gehüllte Rätsel endlich erraten ist, so kann man nicht umhin, einzugestehen, dass auch der Rösselsprung keine verwerfliche, sondern vielmehr eine höchst ergötzliche Unterhaltung ist, welche den Scharfsinn verfeinert und die Denkungskraft erhöht.Zum Schlusse sei uns noch vergönnt zu erwähnen, dass der Herr Verfasser*) dieser Rösselsprünge wohl unfehlbar der einzige sein dürfte, welcher in solcher Mannigfaltigkeit dem Rösselsprung so gefällige Formen gegeben, und selbst das möglich gemacht hat, woran man bisher zweifelte: nämlich Rösselsprünge zu finden, die ganz regelmäßig, dabei aber so künstlich konstruiert sind, dass es Jedermann frei steht, jede beliebige Linie der Zeichnung zu öffnen, von dort aus des Rössleins Sprünge zu beginnen, und so das ganze Schachbrett zu bedecken, dass der letzte Sprung mit dem ersten zusammenfällt. Die nachfolgende Zeichnung aber, in der die Sprünge des Rössleins in zwei Hälften geteilt sind, bei welchen ein jeder Zug des einen Teiles mit dem des andern Teiles gleich ist, sollen tatsächlich unsere Angabe bewahrheiten.
Jede beliebige Linie ist zu öffnen; auch ist jede Figur und jede Linie ganz regelmäßig. Man denke sich punktierte Linien als Demarkation der beiden ganz gleichen Figuren.
*) Collini - Solution du probleme du cavalier au jeu des échecs par Mr. C....
(d. i. Cosimo Alessandro Collini), Mannheim, Tobie Loeffler, 1773. 60 Seiten
Text mit 28 Tabellen.
*) Verfasser H. C. von Warnsdorf - Des Rösselsprunges einfachste und allgemeinste Lösung, gefunden
und dargestellt von H. C. von Warnsdorf, kurfürstlich hessischem
Obergerichtsdirektor zu Fulda. Mit 96 Figuren in Steindruck. Schmalkalden, in
der Th. G. Fr. Varnhagenschen Buchhandlung, 1823. 68 Seiten Text.
*) Der Verfasser des abgebildeten Rösselsprungs ist der Graf Arnold Pongrácz zu
Balassa Gyarmath, auch bekannt unter dem Pseudonym = Einsiedler von Tyrnau.
Der ungarische Schachkomponist Graf Arnold Pongrácz (Pseudonym: Einsiedler von Tyrnau), geboren am 18. Juli 1811 auf Schloss Nedec, gestorben am 7. Juli 1890 in Nagyszombat (ung.) Trnava, deutsche Aussprache: Tyrnau.
1859 unter dem Titel De la solution la plus parfaite du problème du cavalier
veröffentlicht Carl Friedrich von Jaenisch seine symmetrische magische
Springertour im New Yorker Schachmagazin The Chess
Monthly (Band 3, Seiten 110 - 115, 146 - 151 und 176–179). Der Text erschien
zweisprachig in französisch und englisch. Hier zeige ich die die ersten drei
Diagramme von insgesamt sechs:
Anfang A8 - C7
Schach tönt der Feldruf, auf! erwacht,
Ihr Männer all' zur heißen Schlacht,
Ihr Ritter, im Galopp voran,
Ihr Läufer greift die Flanke an,
Ins Zentrum, Rochen, dran und drauf!
Auf, Königin, brich siegend auf,
Mit Allem, was noch Leben hat,
Schach, Schächin biet' ich, Schach und Matt.
|
|